Assessing college lecturers’ mathematical thinking competency, Revista Publicando, 6 (19), 2019, 24-39. ISSN 1390-9304.
Assessing college lecturers’ mathematical thinking competency
Evaluación de la competencia de pensamiento matemático en profesores universitarios
Recibido: 8/ 10 /2018
Aceptado: 19 /12 /2018
Cheong Tau Han1*, Teoh Sian Hoon2, Parmjit Singh3
1 Universiti Teknologi MARA, Kampus Puncak Alam, Selangor, Malaysia, mchgtauhan@gmail.com
2 Universiti Teknologi MARA, Kampus Puncak Alam, Selangor, Malaysia.
3 Universiti Teknologi MARA, Kampus Puncak Alam, Selangor, Malaysia
Resumen: Hay cierta tendencia en el sector privado y las industrias que se hace eco de que los graduados de hoy en día no pueden pensar, no pueden hablar bien y carecen de habilidades sociales. Algunos graduados universitarios no se desempeñan en su trabajo porque tienen pocas habilidades para resolver problemas. Muchos investigadores y educadores han comenzado a estudiar la raíz de la causa. Varios informes han demostrado que la mayoría de los graduados carecen de habilidades de resolución de problemas y de comunicación. Además, también carecen de habilidades de pensamiento. Una de las habilidades de pensamiento de las que carecen los graduados es el pensamiento matemático. Este estudio examina si el nivel de pensamiento matemático de los instructores universitarios es adecuado para educar y producir un pensador matemático. Un total de 128 profesores universitarios de una universidad local han sido elegidos para participar en este estudio. El resultado de este estudio reveló que los logros de los profesores están por debajo del promedio. No tuvieron un buen desempeño en la prueba de pensamiento matemático.
Palabras clave: Pensamiento matemático, pensadores, matemática, competencia del profesorado.
Abstract: Lately, private sectors and industries give feedback that graduates nowadays cannot think, cannot speak well and lack soft skills. Some university graduates fail to perform in their work because they have poor problems-solving skills. Many researchers and educators have started studying the root of the cause. Various reports have shown that most of the graduates’ lack of problem-solving skills and communication skills. Besides, they also lack thinking skills. One of the thinking skills that graduates lack is mathematical thinking. This study examined whether the level of mathematical thinking of college instructors are adequate to educate and produce mathematical thinker. A total of 128 college lecturers from a local university have been chosen to participate in this study. The result of this study unveiled that the achievements of the lecturers are below average. They did not perform well in the mathematical thinking test.
Keywords: Mathematical thinking, thinkers, mathematics, lecturers’ competency.
Devlin (2012) stated that one of the aims of mathematics teaching and learning for the 21st century is the development of mathematical thinking skills yet many researchers and teachers agreed to teach mathematics through a variety of activities. However, some educators have the misconceptions that teaching mathematics using chalk and talk method is equivalent to developing mathematical thinking skills. One should know that learning does not limit to learning additions and expanding new concepts from the existing ones but also involves the learners’ thinking process (Palanisamy K Veloo & Parmjit Singh, 2017).
Mathematical thinking is an abstraction process of fundamental mathematics concepts using non-routine problems in solving problems (Parmjit S., Syazwani Rasid, Nurul Akmal, Teoh S.h. & Cheong Tau Han, 2017). It is a whole way of looking at things, of stripping them down to their numerical, structural, or logical essentials, and of analyzing the underlying patterns. However, why mathematical thinking? One of the major aims of mathematical learning, especially at the tertiary level, is towards the development of mathematical thinking. According to Ridgway (Ridgway, J., Swan, M., & Burkhardt, H., 2001), thinking mathematically is about developing habits of mind that are always there when you need them - not in a book you can look up later. It is pre-built thinking in the mind of an individual when solving problems.
Research has shown that college students are getting good math grades in their transcript. However, it is not being translated into the development of mathematical thinking. Many undergraduate students go to college and university have to study the interconnections of mathematics with other relevant areas of mathematical application such as Physics, Chemistry, Engineering, Computer Science, etc. The syllabus of the programs mainly focusses on content knowledge such as theory, definitions, properties, and algorithm to ensure students can identify and apply this knowledge correctly. The knowledge is based on a formal mathematical algorithm, procedures, and concepts seem remote compared to the concepts students who learn them (Parmjit, S. 2002, 2009, 2006).
University programs are exam-oriented, spawning tutorial sheets, and instructional emphasis which aim in developing computation skills. Students are mainly trained in doing numerical computation, not in making connections to think and solve the problem. Wheatley (1991) stated that students might “stop thinking about the mathematical relationship” together. This is further supported by Hanford (2011) who stated that research conducted over the past few decades show it’s impossible for college students to take in and process all the information presented during a lecture and yet this is one of the primary ways college and university students are taught.
Recently, employer expressed their dissatisfaction to the media towards about local graduates as they failed to meet employer’s expectation (Zafir Mohd Makhbul, Ishak Yussof & Abd Hair Awang (2015). They claimed the graduates could not think and make connections to solve problems. The employers pinpoint and blame the universities for producing graduates who are not thinker and problem solvers. Many studies have found that students’ achievement and performance are strongly correlated with the quality of instructors (Long, C.S, Z. Ibrahim and T.O Kowang, 2013 & Metzler, J. and L. Woesmann, 2012). Thus, this study was undertaken to assess is level of mathematical thinking of university or college lecturers in answering non-routine, problems require mastery in mathematical concepts and principles in advance (Abdul Halim Abdullah, Sharifah Nurarfah S. Abd Rahman, Mohd Hilmi Hamzah, 2017), mathematical thinking test.
Aims of the study: This study aims to assess university or college lecturers’ mathematical thinking and reasoning capabilities in solving non-routines problems. The objectives can be addressed explicitly as below:
• What is the level of university or college lecturers’ attainment in answering mathematical thinking test?
• Are there any significant differences between mathematics lecturers and non-mathematics lecturers (engineering lecturers) thinking skills?
This study employs a quantitative method using a descriptive research design via a paper and pencil test among 128 college lecturers who teach diploma students in four different campuses in Malaysia. They are lecturers who teach in mathematics subjects such as Calculus I, Linear Algebra and other mathematics subjects at the faculty. Besides, there are also some engineering lecturers who teach engineering subjects were selected to participate in this study. This enabled the researchers to evaluate the difference in the thinking skills between mathematics lecturers and non-mathematics lecturers. The four campuses were identified by college management whereby to conduct mathematical thinking courses at the college. The sample was randomly selected based on the list provided by management.
A mathematical thinking test comprising 10 non-routine items were used, as shown in Table 1. Instructors were required to sit for this test to access their mathematical thinking. Calculators were not allowed in the test. The test is constructed based on four domains in mathematical thinking. There are Reasoning and Proof, Communication, Connections, and Representation.
Table 1: Items in Mathematical Thinking Test.
|
#
|
Questions
|
|
1
|
If it takes six men to paint a house in 21 days, how many men does it take to paint the house in 14 days?
|
|
2
|
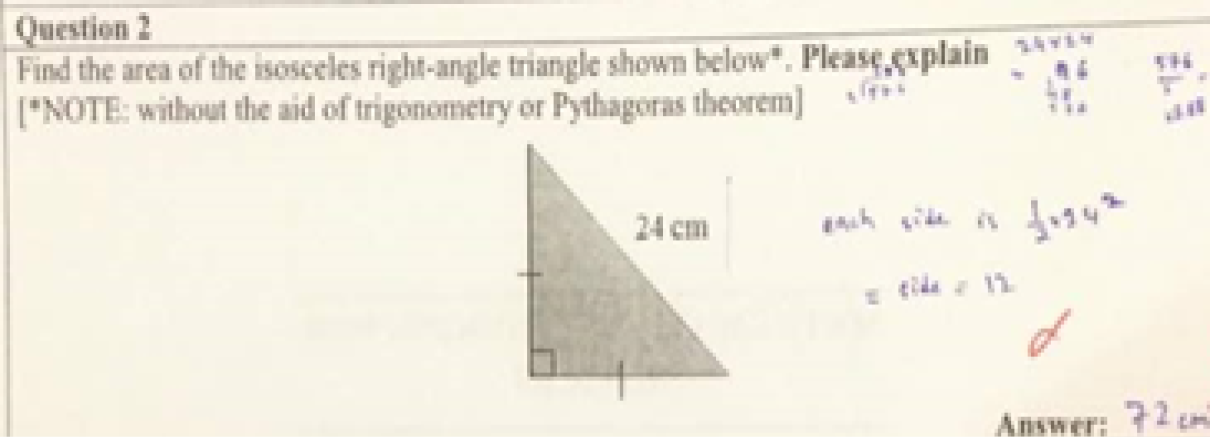
Find the area of the isosceles right-angle triangle shown below*. Please explain.
[*NOTE: without the aid of trigonometry or Pythagoras theorem]
|
|
3
|
Three water hoses are used to fill a children’s swimming pool. The first hose alone takes 3 hours to fill the pool, the second hose alone takes 4 hours to fill the pool, and the third hose alone takes 12 hours to fill the pool. If all three hoses are opened at the same time, how long will it take to fill the pool? Please explain.
|
|
4
|
The sum of the squares of the first fifty positive integers is 42925. What is the sum of the squares of the first fifty positive even integers?
|
|
5
|
Find the last digit of 3 2007
|
|
6
|
Eva and Alex want to paint the door of their garage. The first mix 2 cans of white paint and 3 cans of black paint to get a particular shade of gray. They add one more can of each. Will the new shade of gray be lighter, darker or the same? Please explain.
|
|
7
|
Jaspreet’s and Sharanpreet’s alarm clock rang at 7.30 a.m. For the remainder of the day, Jaspreet’s alarm clock will ring every 45 minutes, and Sharanpreet’s alarm clock will ring every one hour. What will the time be when both the alarm clocks ring together again?
|
|
8
|
There were some students in the classroom, and a total of 36 handshakes took place among the students. Each student shook hands once and only once with everyone else. How many students were in the classroom?
|
|
9
|
What is the next three terms for: 10, 40, 90, 61, 52, 63, ---
|
|
10
|
1 + 2 + 3 + 4 + …….. + 94 + 95 + 96 + 97
When the first 97 whole numbers are adde, what is the digit in the ones place of this total?
|
3. Results and discussions
Table 2 shows the item analysis based on campuses and correct responses. The values in the brackets reflect the number of respondents who answered correctly for the particular item.
Table 2: Item analysis of Mathematical Thinking Test based on campuses and correct responses.
|
#
|
Correct
|
Incorrect
|
|
1
|
13.3% (17)
|
86.7%(111)
|
|
2
|
14.1% (18)
|
85.9%(110)
|
|
3
|
14.1%(18)
|
85.9%(110)
|
|
4
|
6.3%(8)
|
93.8%(120)
|
|
5
|
22.7%(29)
|
77.3%(99)
|
|
6
|
26.6%(34)
|
73.4%(94)
|
|
7
|
60.90%(78)
|
39.1%(50)
|
|
8
|
15.6%(20)
|
84.4%(108)
|
|
9
|
1.6 (2)
|
98.4%(126)
|
|
10
|
13.3% (17)
|
86.7%(111)
|
Overall mean score: 1.83
Overall standard deviation: 1.32
maximum score: 10
The finding in table 2 shows the university lecturers facing difficulty in answering the mathematical thinking test. Overall, the participants obtained low marks for all the items. However, a high percentage (60.90%) of the participants successfully answered item 7. This shows that many of the participants applied knowledge of common multiple (which is a concept learned and applied since Form One). It also shows that recalling previous knowledge becomes part of the process of solving the problem. Nevertheless, the results for the rest of the items do not show an average performance, as indicated in item 7. This indicates that when more reasoning based on existing knowledge (such as proportion or percentage) is required, the participants failed to generalize the situation as stated in the problem. This can be justified through their performance in item 6 (26.6%) and item 5 (22.7%). Lower performance was also shown in item 8 (15.6%), item 2 (14.1%), item 10 (13.3%) and item 1 (13.1%). The result also shows an exceptionally low percentage of participants managed to answer item 4 (6.3%) and item 9 (1.6%). These two items involve the process of reasoning and pattern searching. Hence the lack of specific skills (reasoning and pattern searching) failed in solving items 4 and 9.
Item analysis: This study details the errors made by the lecturers who took part in the Mathematical Thinking Test. Due to constraints of space, only five questions will be discussed.
Item 1: If it takes six men to paint a house in 21 days, how many men does it take to paint the house in 14 days? The findings in table 2 show that only 13.3% of respondents answered this question correctly.
86.7% of the lecturers applied direct proportional thinking method by using cross multiplication method (refer to figure 1). This shows that the lecturers emphasize the algorithmic procedure. They did not check whether the answer makes sense. Many of the apply the following heuristic
• 21 men need 6 days
• 14 days need x men
• x/6=14/21, 21x=84, x=4
The solution to this problem as below:
• To paint a house, need 21x6=126 men days
• To paint the same size house, need 14x9=126 men days.

Error A

Error B
Figure 1: Errors for item 1
Item 2: Find the area of the isosceles right-angle triangle shown below*. Please explain.
[*NOTE: without the aid of trigonometry or Pythagoras theorem]

For this item, only 14.1% of respondents answered correctly. More than 40% of the respondents still applied the trigonometry and Pythagoras theorem in solving this item (refer to figure 2). This shows that lecturers relied on the formula and theorem they have memorized. They lack geometrical sense in expanding the right triangle into a square. The area of the square is 24x24=576 cm2 (refer figure 2.1) and the area of the triangle is a quarter area of the square which is 144cm2.
Item 3: Three water hoses are used to fill a children’s swimming pool. The first hose alone takes 3 hours to fill the pool, the second hose alone takes 4 hours to fill the pool, and the third hose alone takes 12 hours to fill the pool. If all three hoses are opened at the same time, how long will it take to fill the pool? Please explain.

Error A
Error B
Figure 2: Errors in item 2

Figure 2.1 Geometry expansion
The data in table 2 show that only 14.1% of the respondents answer correctly. 86% of the respondents could not answer this question correctly. They left the question blank. However, it is found that some engineering lecturers did answer less than 3 hours even though no exact answer provided. This shows that these engineering lecturers used common sense in answering and designing. The solution to this question is 1.5 hours.

Error A

Error B
Figure 3: Errors for item 3.
Item 4: The sum of the squares of the first fifty positive integers is 42925. What is the sum of the squares of the first fifty positive even integers?
The data in table 2 show that item 4 has the second lowest score among the 10 items. 94% of lecturers did not answer this question. The Malaysian school syllabus contains arithmetic progression but does not contain the square of an arithmetic progression. Most respondents did not notice that the sum of squares of the first fifty positive even integers is four times the sum of the squares of the first fifty positive integers (refer figure 4). The solution is as shown below:


Error A
Figure 4: Error for item 4
Item 9: What are the next three terms for 10, 40, 90, 61, 52, 63.
Table 2 shows that item 9 has the lowest score among the 10 items.
98% lecturers failed to identify the pattern from the sequence. They have wrongly applied arithmetic, geometric, and harmonic rules in analyzing the sequence. They have neglected the directions to analyze the sequence. Most of the time, human beings read from left to right, but to solve this problem, one needs to read from right to left. Surprisingly, a pattern can be identified. The solution of the question is 94, 46 and 18 (refer to figure 5)

Error A

Error B
Figure 5: Errors for item 9
Other than looking at the errors made by the respondents, it is necessary to identify the significant differences in mathematical thinking between mathematics lecturers and non-mathematics lecturers.
Table 3 shows the independent sample t-test finding of two groups of respondents.
|
N
|
Mean
|
SD
|
t
|
df
|
Sig
|
|
Math lecturer
|
68
|
1.83
|
0.12
|
0.203
|
112
|
0.840
|
|
Non-mathematic lecturer
|
60
|
1.54
|
0.18
|
|
|
|
The results show that there is no significant difference in the thinking skills between mathematics lecturers and non-mathematics lecturers as the p-value is higher than 0.05. This means that both mathematics and non-mathematics lecturers have similar thinking skills because there is no significant difference in answering the Mathematical Thinking Test.
The findings of this study reveal that both mathematics and non-mathematics lecturers have deep mathematical thinking. They are the facilitators and instructors for most of the subjects at the tertiary education level. If their mathematical thinking competency is low, do they capable to educate and producing mathematical thinker? (Leron & Hazzan, 1997) Can they trigger student’s competency?
Mathematics lecturers always have high pride in solving most mathematics problems. However, the findings of this study show that most of the lecturers focus on algorithm procedure to solve problems without even thinking if the solutions make sense. Respondents did not apply Polya’s reflection to double check their solution. This can be seen from item 1. This is common and logical that more people are needed to paint a house in a shorter time frame. However, most respondents did not think in such a way.
Hughes-Hallet highlighted that a person must first develop problem-solving skills before acquiring mathematical thinking skills. Leron (Muzenda, 2013) pointed out that learners’ ability in solving a mathematical problem is much affected by their behavior in solving mathematical tasks taking into account their attempts in understanding the task and handling the failure for such attempts. Therefore, to overcome the problem, instructors must first involve themselves in solving problems that are interesting, stimulating and challenging without the aid of any calculators or even any sophisticated formulae's which will inadvertently develop their thinking. Once they start thinking out of the box, they will then change their conventional lecture towards conceptual understanding.
A thinker instructor will always steer his students towards a creative and innovative thinker.
Acknowledgments
The researchers would like to express their gratitude to Institute of Research Management and Innovation (IRMI), Universiti Teknologi MARA for financing this research and support rendered for the RIG Mathematical Thinking for Teaching Research Group (600-RMI/DANA 5/3/REI (17/2015).
Abdul Halim Abdullah, Sharifah Nurarfah S. Abd Rahman, Mohd Hilmi Hamzah (2017). Metacognitive Skills of Malaysian Students in Non-Routine Mathematical Problem Solving, Bolema: Boletim de Educação Matemática, 31, (57).
Devlin, Keith (2012). Introduction to mathematical thinking, Keith Devlin, United Kingdom. Retrieved from https://www.coursera.org/learn/mathematical-thinking
Emily Hanford (2011). Rethinking the Way College Students Are Taught. Retrieved from http://americanradioworks.publicradio.org/features/tomorrows-college/lectures/ rethinking-teaching.html
Leron and Hazzan (1997). The world, according to Jolnmy: A coping perspective in mathematics education. Educ. Stud. Math. (32), 265-292.
Long, C.S, Z. Ibrahim and T.O Kowang (2013). An analysis of the relationship between lectures’ competencies and student’s satisfaction. Int. Edu Stud, (7), 37-46.
Metzler, J. and L. Woesmann (2012). The impact of teacher subject knowledge on student achievement: Evidence from within-teacher within students’ variation, J. Dev. Econ, (99), 486-496.
Muzenda, Allexander (2013). Lecturers’ Competences and Students’ Academic Performance, International Journal of Humanities and Social Science Invention, 3 (1), 06-13.
Palanisamy K Veloo, Parmjit Singh (2017). “Using Representations to Develop Mathematical Thinking,” Empowering Mathematics Learners, Yearbook, Association of Mathematics Educators (Chapter in the book).
Parmjit S., Syazwani Rasid, Nurul Akmal, Teoh S.h, Cheong Tau Han (2017). How Well Do University Level Courses Prepare Students to be mathematical thinker, The Social Sciences, 12, (9), 1516-1521.
Parmjit, S. (2002). Orientations of school mathematics in Malaysia. J. Pendidikan, (18), 58-64.
Parmjit, S. (2009). Variation in first-year college students understanding on their conceptions of and approaches to solving mathematical problems. Asian J. Univ. Educ., (5), 95-118.
Parmjit, S., and W. Allan. (2006). Unpacking first-year university students mathematical content knowledge through problem-solving, Asian J. Univ. Educ, 2:33-56.
Ridgway, J., Swan, M., & Burkhardt, H. (2001). Assessing Mathematical Thinking via FLAG. In D. Holton and M.Niss (eds.): Teaching and Learning Mathematics at University Level - An ICMI Study. Dordrecht: Kluwer Academic Publishers.
Wheatley, G.H. (1991). Constructivist perspectives on science and mathematics learning. Sci. Educ., (75), 9-21.
Zafir Mohd Makhbul, Ishak Yussof & Abd Hair Awang (2015). Antara realiti dan harapan – Kajian empirikal persepsi majikan terhadap prestasi graduan tempatan, GEOGRAFIA OnlineTM Malaysian Journal of Society and Space, 11, (10), 27-36.











